Kuppelkonstruktionen aus Bambus

Intro

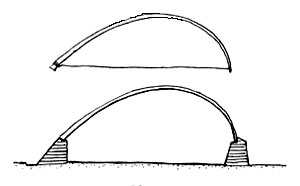
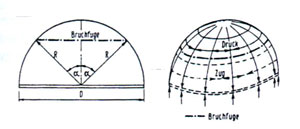
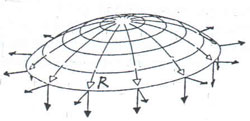
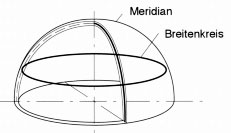
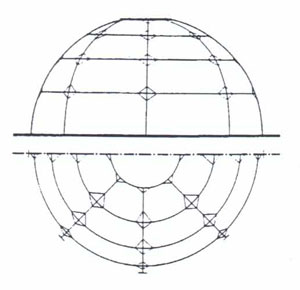
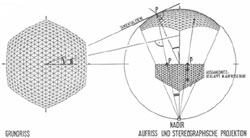
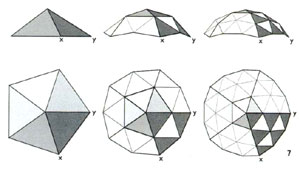
Hagia Sophia	Kuppel sind in ihrer räumlichen Gestalt "Wölbungen über einen Raum mit runder, recht- oder vieleckiger Grundfläche in Form einer Halbkugel (Kugelkuppel) oder anderer Kugelabschnitte (Flachkuppel, Spitzkuppel, Prismenkuppel)".
Pantheon/ Rom	Im Laufe der Geschichte wurden für Kuppeln zahlreiche Tragsysteme entwickelt und unterschiedliche Materialien eingesetzt. Am Anfang steht die massive Kuppel aus behauenem Stein, Ziegeln oder unbewehrtem Beton.
Stadion in Rom/ Nervi	Statisch gesehen sind Kuppeln sind doppelt gekrümmte Schalen. Druck-, Zug, und Schubkräfte werden in der Schalenfläche abgetragen. Die massive tragende Kuppelschale kann aufgrund ihrer günstigen statischen Wirkung sehr gering bemessen werden, jedoch ist sie dann in ihrer Stabilität gegen unsymmetrische und konzentrische Lasten begrenzt. Aussteifungen in Form von Rippen, die auch einen Teil der Schnittgröße übernehmen, können diesem Problem entgegenwirken.
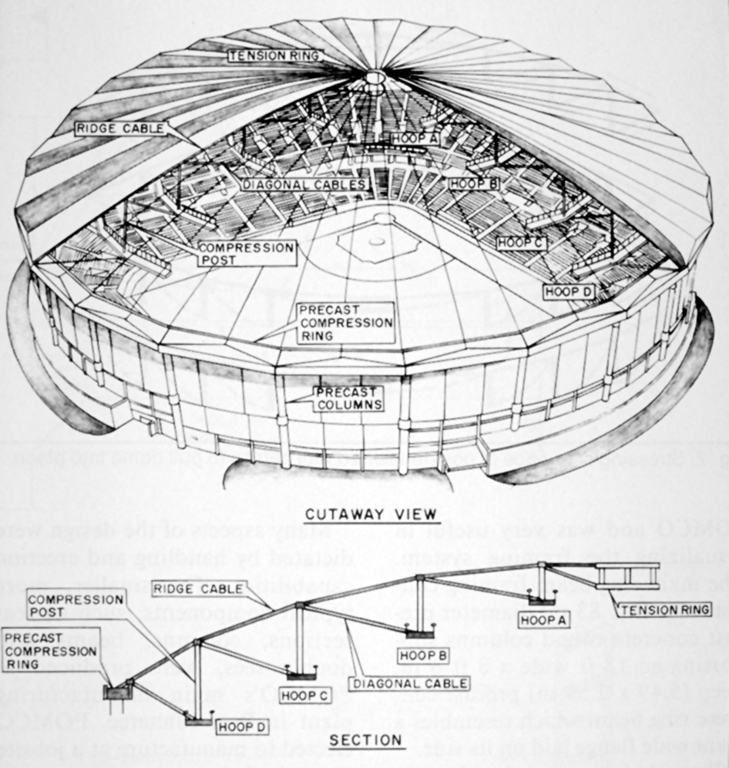
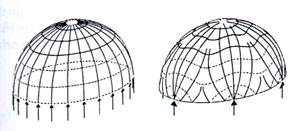
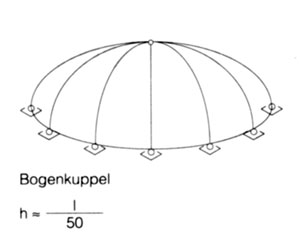
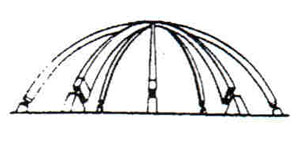
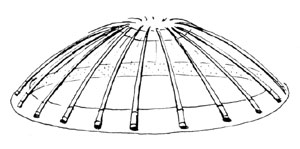
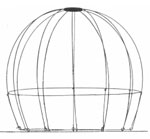
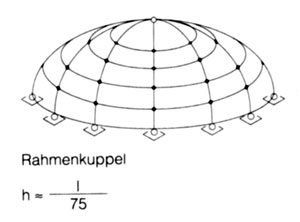
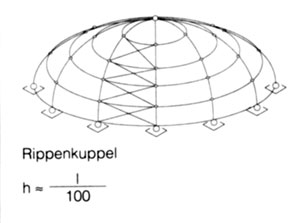
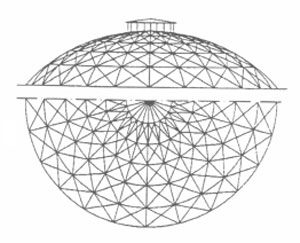
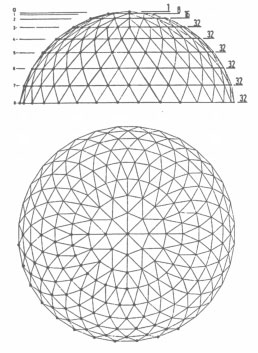
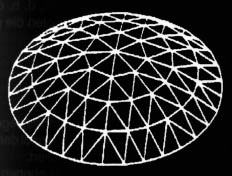
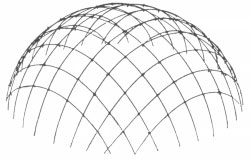
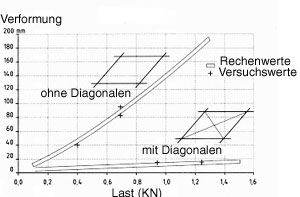
Bewehrung für eine Stahlbetonkuppel	Die konsequente Weiterentwicklung ist ein Stabwerk, das sich von der Fläche "löst" und die Funktion der Schale übernimmt. Die Abdeckung der Kuppel leitet die Lasten direkt an das Traggerüst weiter und muß keine Schalenfunktion übernehmen. Der Vorteil des Stabwerks liegt in seiner Lastumlagerungfähigkeit, dem geringen Materialeinsatz und geringen Gewicht, sowie in der einfachen und schnellen Montage auf der Baustelle.
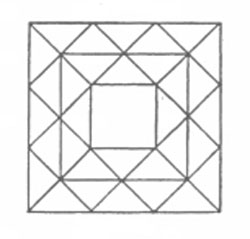
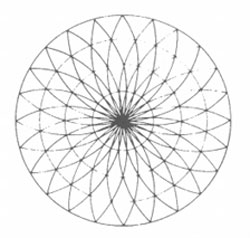
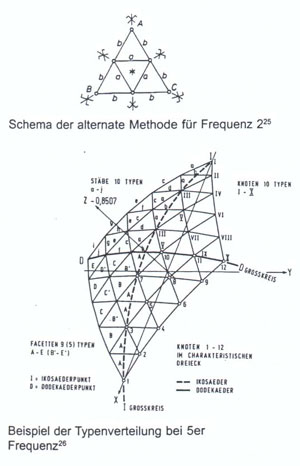
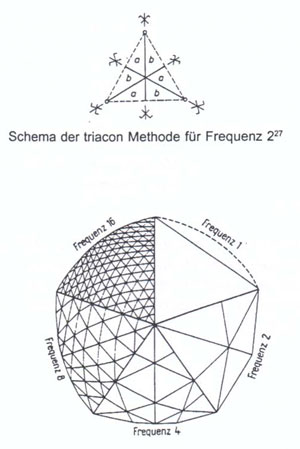
moderne Stahlkuppel	Kuppelstabwerke werden in großem Maßstab aus Holz und Stahl konstruiert. Im folgenden werden verschiedene Kuppeltypen hinsichtlich ihrer Geometrie und ihres Tragverhaltens charakterisiert. Dabei wird untersucht, inwiefern sich Bambus mit seinen spezifischen Eigenschaften als Konstruktionsmaterial für verschiedene Kuppeln einsetzen läßt. Zunächst erfolgen jedoch allgemeine Aussagen zu den Konstruktions- eigenschaften von Bambus, sowie zum Tragverhalten und zur Geometrie und von Kuppeln.

In seiner Eigenschaft, sowohl Druck, als auch Zugkräfte aufnehmen zu können, ähnelt Bambus Stahlstäben und scheint damit generell für die Konstruktion von Kuppelstabwerken geeignet zu sein. Folgende Eigenschaften sind jedoch bei der Planung zu berücksichtigen bzw. lassen sich für den Entwurf spezieller Bambuskuppeln einsetzen :

Wie alle pflanzlichen Stäbe läuft der Bambus in seiner vollen Länge zur Spitze hin konisch zu. Bei der Verwendung gerader Stäbe wird deshalb hauptsächlich der untere, steifere Teil verwendet.

In einigen Konstruktionen, besonders beim Einsatz gekrümmter Stäbe, ist es jedoch sinnvoller, die volle Stablänge des Bambus zu verwenden und den konischen Wuchs des Bambus im Entwurf zu integrieren. Dabei kann die charateristische, asymmetrische Biegelinie beim Kuppelbau als Inspiration dienen.

Die Schwierigkeit bei der Konstruktion von Bambusstabwerken liegt eindeutig bei der Ausbildung der Knoten, insbesondere bei dreidimensionalen und auf Zug belasteten Verbindungen. Wegen Faserstruktur des Bambus fransen Bohrungen schnell aus, bei ringförmigen Einfassungen werden die Halme zusammengedrückt.

Textile Verbindungen können dem Anspruch komplexer Konstruktionen kaum genügen. Sie werden hauptsächlich bei temporären Bauten eingesetzt.

Mögliche Verbindungen für Bambuskuppeln werden im Anschluß an die Typenbeschreibung aufgeführt und untersucht.

Tragverhalten von Kuppeln

	Kuppeln verfügen aufgrund ihrer doppelten Krümmung über ein sehr günstiges Tragverhalten. Gleichmäßig verteilte Belastungen werden ausschließlich über Axialkräfte abgetragen. In Meridianrichtung treten nur Druckkräfte auf; in Ringrichtung treten im oberen Bereich der Kuppel Druckkräfte und unterhalb des Bereiches Zugkräfte auf. Der Übergang zwischen den beiden Zonen ist die Bruchfuge.
	Jede Kuppel, die flacher als eine Halbkugel ist, benötigt eine spezielle Randlagerung, die auch Horizontalkräfte aufnehmen muß.
	Der Kräfteverlauf innerhalb der Kuppel hängt auch von ihrer Lagerung ab. Nur bei einer kontinuierlichen Lagerung wirkt die Kuppel als Schale. Jede Unterbrechung der Lagerung erzeugt einen ungleichmäßigen Kräfteverlauf.

Geometrie

radial- konzentrisch, homogen, geodätisch

Kuppeln lassen sich in eine Vielfalt von Stabwerken auflösen.

Die Einteilung der Kugeloberfläche in möglichst viele gleiche Stablängen stellt jedoch ein geometrisches Problem dar, da sich die Teilung nicht abwickeln läßt. Es bieten sich daher drei räumlich ansetzende Systematiken an:

- radial- konzentrisches Prinzip

- Geodätisches Netz

- Homogennetz

Die Wirtschaftlichkeit von Kuppeltragwerken bedingt sich durch die Wahl des Stabwerks. Das Optimierungsziel ist eine geringe Anzahl unterschiedlicher Knoten- und Stabtypen. Da sich Bambus - lapidar gesagt - leicht sägen, aber schwer zu Stabwerkknoten verbinden läßt, sollte das Minimieren der Knotentypen das erste Ziel sein.

Radialkonzentrische Kuppeln

Die Oberfläche der Kuppel ist in ein Netz aus Längen- und Breitenkreisen eingeteilt. Die Längenkreise oder Meridiane sind Radialen, die sich von Pol zu Pol erstrecken und sich in den Polen schneiden. Von den Breitenkreisen entspricht der Äquator dem Durchmesser der Halbkreiskuppel, die übrigen Kreise werden polwärts immer kleiner.

Radial- konzentrische Kuppeln eignen sich aufgrund ihrer Stab- und Knotenvielfalt nur sehr bedingt für Bambuskontruktionen. Dennoch werden die verschiedenen Typen hier vorgestellt. Die einfachsten Formen sind auch in Bambus machbar.

Bogenkuppel

	Radiale, gekrümmte Rippen bilden die Tragstruktur, die über Flächenelemente ausgesteift wird. Die Rippen nehmen als Hauptträger wie Bogensegmente die Lasten auf.
	Die konzentrischen Rippen treffen sich alle im Pol. Es entsteht dadurch eine komplizierte Anschlußsituation.
	Bogenkuppeln aus Bambus sind auf jeden Fall denkbar. Der komplizierte Polanschluss kann wie in der Abb. durch einen abschließenden Druckring umgangen werden.
	Bambusspezifische Formen entstehen, wenn die Enden eingespannt und die biegsameren Spitzen zusammengeschlossen werden. Durch die gelenkige Lagerung mit einem Zugband und zusätzlichem Druckring erhält die Kuppel eine größere Steifigkeit. Es bildet sich eine bauchigere Form mit nach außen geneigten Bogenansätzen.

Rahmenkuppel

Die Kreuzpunkte zwischen den radial verlaufenden Stäben und den Breitenkreisen sind biegesteif ausgeführt. Die durchlaufenden Rippen werden durch die horizontalen Stäbe ausgesteift.

Die Stablängen der horizontalen Ringe sind jeweils gleich. Wie bei der oben aufgeführten Rippenkuppel kommt es im Pol zu einer problematischen Stabverdichtung. Diese kann umgangen werden, indem der Abschluß als Druckring ausgebildet und damit der Zenit ausgespart wird.

An den biegesteifen Knoten werden recht große Momente übertragen, Stäbe und Knotzen müssen daher entsprechend stark dimensioniert werden. Das Tragwerk eignet sich deswegen nur für kleine Spannweiten, es ist material- und montageaufwändig.

Bei durchlaufenden Radialen und gestoßenen Querstäben treten große Querkräfte auf, die Bambushalme aufgrund ihre Rohrquerschnitts nicht aufnehmen können.

Schwedlerkuppel

	Die Flächen zwischen den radialen und den Horizontalen werden durch Diagonalen ausgesteift. Die durch die Diagonalen gebildeten Dreiecke eines Gefaches liegen in einer Ebene. Werden die Diagonalen kreuzweise geführt, kann man sie durch Seile ersetzen, was das Ablängen der Diagonalstäbe erspart.
	Das Anwenden von Seilen eignet sich besonders für Bambuskonstruktionen, da so das mühsame Ablängen zu vieler Stäbe entfällt. Für die gelenkigen Anschlüsse der Rippen und Querstreben gilt das typische Anschlussproblem.

Dreiläufige Ringnetzkuppel

Die horizontalen Breitenringe werden durch zwei weitere, diagonal verlaufende Stabscharen so verbunden, dass gleichschenklige Dreiecke entstehen. Durch die dreieckige Grundform entsteht eine hohe Steifigkeit, die zu ökonomisch günstigen Systemen führt. Leider gibt es auch hier eine ungänstige Verdichtung der Stäbe zum Zenit hin.

Ausser der Aussparung des Zenits durch einen Druckring gibt es bei radialen Netzen zwei weitere Möglichkeiten, die Stabverdichtung zu umgehen:

Bei der sogenannten Zonenetzkuppel wird im Zenit eine Übergangszone eingeführt, in der die Stabanzahl durch fortschreitende Halbierung beseitigt wird.

Das Ringnetz besteht aus zwei Teilen: der Polzone als Kuppelabschluß und der Breitenzone mit horizontalen Ringen und zwei Scharen spiralförmig verlaufender Diagonalen.

Eine weitere Möglichkeit ist die Ausbildung einer Sektornetzkuppel. Ihre Obefläche wird in Sektoren geteilt, die durch Scharen von parallel zu ihren Begrenzungslinien verlaufenden Stäben unterteilt werden.

Gitternetzkuppel

	Diese Kuppel verfügt über ein quadratisches Grundraster, das sich zu Rauten verezerrt, sobald es in Kuppelform gebracht wird. Die Form entspricht der Umkehrung der Kettenlinie. Hinsichtlich seiner Geometrie ist die reine Gitternetzkuppel keine radial- konzentrische Kuppel, sondern setzt sich sich aus Kreisen zusammen, die sowohl in vertikaler als auch in horizontaler Richtung kleiner werden. Bei diesem System reicht eine Stablänge aus, dafür entsteht eine Vielzahl unterschiedlicher Felder.
	Um die Schalentragwirkung herzustellen müssen die Rauten durch Diagonalen ausgesteift werden. Die Ausbildung der Diagonalen durch abgelängte Stäbe wäre aufgrund der vielen unterschiedlichen Felder und Diagonallängen unwirtschaftlich. Es reicht jedoch bei diesen Kuppeln, durchlaufende Seile an den Knoten festzuklammert.
	Die Anschlußstellen der Gitternetzstäbe scheinen zunächst im Vergleich zu den Verbindungen anderer Kuppeln unkompliziert: es treffen immer nur zwei Stäbe aufeinander. Allerdings muss die Verbindung so ausgebildet werden, dass sie sich verdrehen und nach der Kuppelformung fixieren lässt.
	Stahlstäbe werden einfach miteinander verschraubt, bei Bambusnetzen gestaltet sich der Verbindungsvorgang um einiges schwieriger. Bislang wurde nur mit textilen Verbindungen experimentiert. Die Fixierung der gebundenen Knoten wurde dabei durch zementgetränkte Bandagen und durch zwischengelegte Gummischeiben vorgenommen.
	Um die Kuppel z. B. im Gebäude als Dach einsetzen zu können, bedarf es eines Zugringes, der die Kuppel einfaßt. Für Herstellung dieses Ringes wie auch für größere Spannweiten des Gitternetzes werden es zusammen- gesetzte Bambusstäbe benötigt. Auch hier ist die Verbindung der Knackpunkt. Im Endeffekt scheitern jedoch die Konstruktionen aus ganzen Bambushalmen hauptsächlich an der leichten Spaltbarkeit der Stäbe. Benötigt werden hier leicht biegsame Vollprofile kleineren Durchmessers, die sich zu beliebigen Längen zusammensetzen lassen.
	Gespaltener Bambus eignet sich durch seine bessere Biegbarkeit im Grunde besser für die Konstruktion von Gitternetzkuppeln, allerdings ist die Spannweite auf etwa 10m begrenzt.

Homogennetzkuppel

Bei einem Homogennetz schließen an jedem Knoten die gleiche Anzahl von Stäben an.

"Ein in der Äquatorialebene einer Kugel lokalisiertes Dreiecksnetz wird vom Nadirpunkt (Gegenpol der Kugel) auf den Polbereich der Kugeloberfläche projeziert."

Projektion

Dabei bilden sich drei Gradenscharen des ebenen Netzes auf drei Kleinkreisscharen des sphärischen Netzes ab, wodurch das Netz eine recht harmonische Wirkung erhält. Da es sich bei steileren Kuppeln am Rand zu stark verzieht und damit ungünstig große Stablängen erzeugt, ist das System nur für flachere Kuppeln geeignet.

Geodätische Kuppeln

	Zu einer innovativen Einteilung der Kugeloberfläche kam Anfgang des 20. Jahrhunderts Buckminster Fuller (links bei einem praktischen Versuch mit Studenten): die Oberfläche der Kugel wird durch die mehrfache Unterteilung eines Ikosaeders erreicht.
Tetraeder, Hexaeder, Oktaeder, Dodekaeder, Ikosaeder	Das Ikosaeder ist eines der fünf von Platon beschriebenen regelmäßigen Polyeder. Seine Oberfläche ist aus 20 gleichseitigen Dreiecken mit 30 gleich langen Stäben zusammengesetzt und nähert sich der Kugelform.
	Werden die Kanten von innen auf eine Kugeloberfläche projiziert, wird die Oberfläche in zwanzig sphärische gleichseitige Dreicke zwischen Großkreisen aufgeteilt, die in geeigneter Form auf dem Weg über Sechsecke und, in den Ecken der Großdreiecke, Fünfecke mit einem dreieckigen Stabnetz belegt werden. Das Prinzip läßt sich auch auf andere platonische Körper, wie z. B. Dodekaeder anwenden.
Frequenz1, Frequenz 2, Frequenz3	Die Unterteilung des Ikosaeders erfolgt über die Teilung der Dreiecksseiten. Anschließend werden die Teilungspunkte verbunden und damit neue Dreiecke gebildet. Die Anzahl der Teilstrecken wird als Frequenz bezeichnet.
	Zwei Methoden der Unterteilung haben sich durchgesetzt: 1. "Alternate" Methode: Jeder Teilungspunkt einer Ikosaederseite ist Eckpunkt eines Dreiecks (s. a. oben links). Bei einer 8er- Frequenz beispielsweise entstehen 10 unterschiedliche Stablängen und Knotentypen. Die Methode eignet sich besonders für Kugelabschnitte.
	2. "Triacon"- Methode: Nur jeder zweite Teilungspunkt der Ikosaederseite wird Eckpunkt eines Dreiecks. Bei einer 8er- Frequenz entstehen hier 8 unterschiedliche Stablängen und Kontentypen. Diese Methode eignet sich besonders für Vollkugeln. Sie läßt sich nur für gerade Frequenzen anwenden.
	Dieses Beispiel aus IL 31 zeigt eine geodätische Kuppel aus 10- 15 cm dicken Bambusrohren mit einer 2fach- Teilung jeder Ikosaederseite (Frequenz 2), bei dem die oberste Unterteilung ausgespart wurde. Die Gitterschale umspannt 6m. Obwohl sie sehr massig aussieht, wiegt sie nur 2 kN und trägt das hundertfache ihres Eigengewichts.
	Die Schale wurde mit einer vorgespannten Membran aus PVC- beschichtetem Polyestergewebe abgedeckt. Die höchste Stelle der Membran wird durch einen Bambushängestab abgestützt.
	Die einzelnen Bambusrohre sind abgelängt und mit Stahlprofilen verbunden. Das Aufspalten der Stabenden soll durch rostfreie Stahlbänder verhindert werden. Es scheint jedoch, als ob diese mit dem Bambus verbohrt sind, was unweigerlich zu Schwachstellen führt.
	Besonders im Vergleich mit einer geodätischen Stahlkuppel wirkt die Bambuskuppel massig und die Verbindungen sehr aufwendig. Aus Transportgründen im Moment die Verwendung des Bambus in Form kurzer, gerader Stäbe propagiert. (Jörg Stamm) Bei der Anwendung dieser Stäbe für geodätischen Kuppelbauten werden hier sowohl die Wirtschaftlichkeit als auch die Ästhetik in Frage gestellt.

Verbindungssyteme

Entwurf für einen räumliche Knoten/ Renzo Piano- Building Workshop	Für räumliche Knotenstabwerke aus Stahl und Vollholzquerschnitten sind bereits verschiedene Verbindungssysteme entwickelt worden, die sich allerdings nur bedingt für Bambus anweden lassen. Die im Bereich des Möglichen liegenden Verbindunsarten werden im folgenden aufgeführt.
	Bambutec


	Induo: Dieses System eignet sich hervorragend zur Ausbildung von Holzstabwerken.
	Induo ließe sich auf Bambus jedoch nur dann anwenden, wenn die Enden der Rohre mit Zement oder ähnlichem vergossen werden und sich das dornige Ende der Gewindestange verzahnen läßt.
	Ankerschrauben lassen sich auch nur im Bambus vegießen. Für mehrfache Stabstöße müßten auch mehrfache Ankerschrauben entwickelt werden.
	Umfassende Zusammenstellungen von Bambusverbindungen: xxx yyy

Tensegrity im Kuppelbau

Die sogenannten "Cable Domes" sind die einzigen Tragwerke, bei das von Buckminster Fuller entwickelte Tensegrity- Prinzip in großem Maßstab angewandt wird.

bild

Sie setzen sich aus Ringen abgestuften Durchmessers zusammen. Dabei ist jeder Ring mit seiner Unterseite an der oberseite des darunter liegenden größeren Ringes aufgehängt. Mit jeder Aufhängung ergibt sich dadurch ein Höhengewinn. Die Druckkraft zwischen den sich kreuzenden SAeilen übernimmt entweder der Ring selbst, oder seine Druckstäbe leiten sie weiter.

Diese Art von Kuppeln im Zusammenhang mit Bambus- konstruktionen aufzuführen geht wahrscheinlich - wie der Entwurf für die Mendocino- Brücke von DeBoer - ein Schritt zu weit. Es zählt hier auch mehr um der Anspruch auf die Typenvielfalt von Kuppeln.

Literatur

Frei, Otto (Hsg.): "IL 31", Stuttgart 1985

Führer, Wilfried; Heyden, Wilhelm; Dahlhausen, Jochen: "Räumliche Knotenstabwerke", Aachen 2000

Heinle, Erwin; Schlaich, Jörg: "Kuppeln- alle Zeiten- alle Kulturen", Stuttgart 1996

Herzog, Thomas; Natterer, Julius; Volz, Michael: "Holzbauatlas Zwei", München 1991

Peters, Stefan: "Richard Buckminster Fuller" in db 2/ 2002