Analyse mit ExTra CAD

Lastfall Volllast

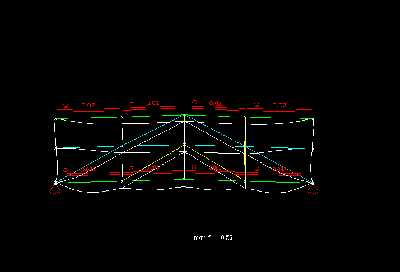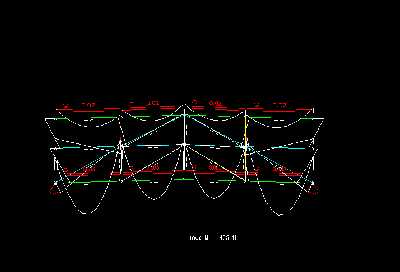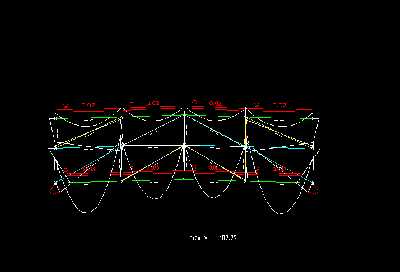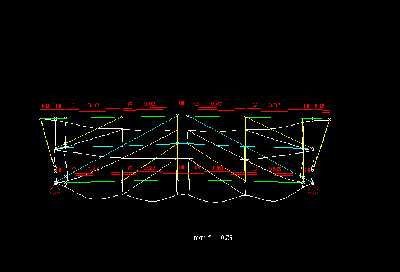
Mit allen Stäben ist das System 73-fach statisch ueberbestimmt und die maximale Durchbiegung beträgt nur noch 0,48cm, was auf die gesamte Spannweite bezogen l/2000 entspricht.
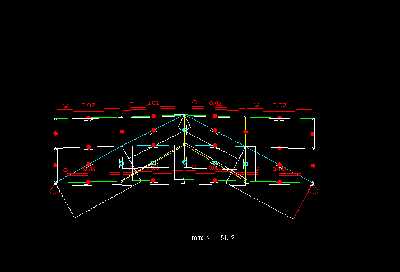
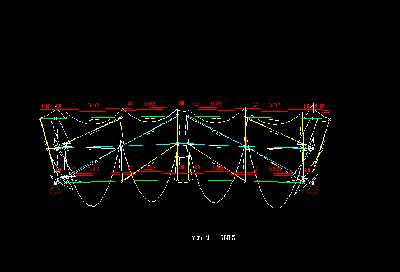
In der ueberhoehten Darstellung der Durchbiegung erkennt man im Untergurt gut eine gleichmaeßige, wellenförmige Durchbiegung, die im Mittelbereich zwischen den Vertikalen am groeßten ist. An den Vertikalstaeben fällt die Verformung deutlich geringer aus und an den doppelten Vertikalen - besonders an den aeußeren Beiden setzt der Durchhang erst viel später ein, was am Obergurt noch weiter durch die Konsolen unterstützt wird. Der Obergurt biegt sich gleichmaeßiger als der Untergurt durch aber die Verminderung der Verformung an den mittleren Vertikalen ist noch zu erkennen. Die Vertikalen, die Diagonalen und die Mittelgurtstaebe haben selbst kaum einen eigene Verformung - sie folgen eigentlich nur dem Durchhang des restlichen Systems.

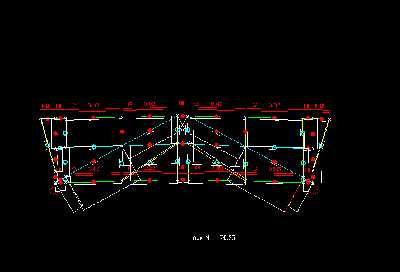
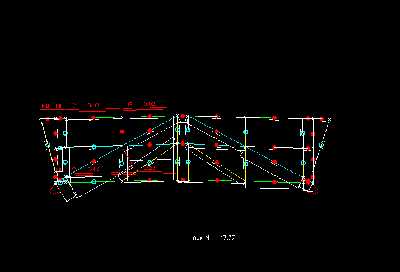
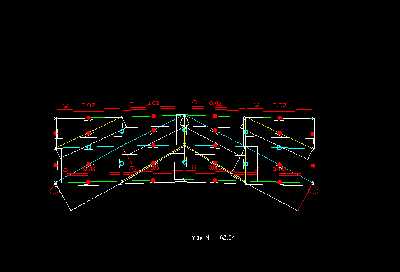
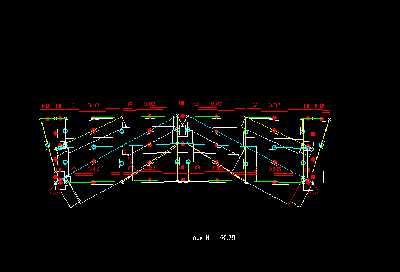
Im Schaubild der Laengskraft kann man - wie auch das System selbst schon und das Bild der Durchbiegung weiter vermuten laeßt, gut erkennnen, daß die meisten Vertikalen und die kleinen Diagonlstaebe auf Zug belastet werden, um Obergurt und Untergurt zusammen zu halten.
Nur der jeweils obere Abschnitt der mittleren Vertikalen, die auf den großen Diagonalen enden, sowie die aeußeren Vertikalen werden zur Stützung des Systems auf Druck belastet. Die auf Druck belasteten Vertikalstaebe werden weniger stark beansprucht als die auf Zug belasteten Staebe. Die Lastabtragung vom Obergurt erfolgt somit komplett über die aeußeren Vertikalen und über die großen Diagonalen, die alle direkt an den Auflagern enden. Mit einem Einzugsfeld von knapp 4m Breite sind die unteren Abschnitte der großen Vertikalen, die am staerksten belastendsten Staebe. Sie leiten die Kräfte von den oberen Abschnitten und von den mittleren Vertikalen in die Auflager. Die Laengskraft betraegt 76,23kN. Die Spannung aufgrund der Laengskraft, die sie aushalten muessen betraegt 0,76kN/cm²

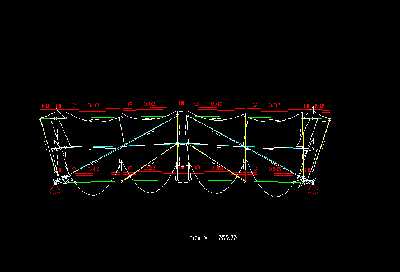
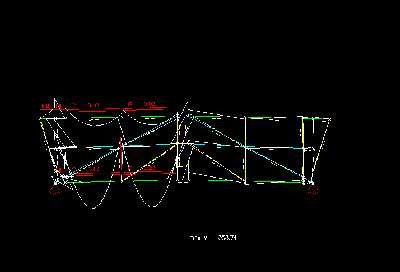
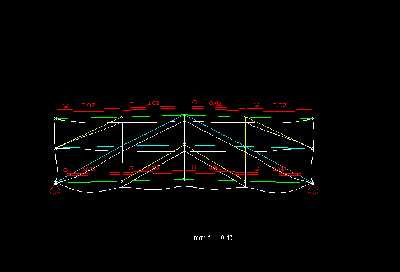
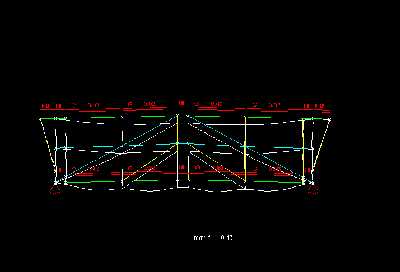
Die Vertikalen, die Diagonalen und die Mittelgurtstaebe - haben wie schon gesagt - selbst kaum eine eigene Verformung. So treten in diesen Staeben auch keine oder nur sehr geringe Momente auf. Am staerksten werden der Ober- und Untergurt verformt. Sie muessen somit auch die groeßten Momente aufnehmen. Auf diesen Staeben liegt auch die Last. Durch die Knoten gleicht die Momentenlinie des Obergurtes und mehr noch des Untergurtes der eines Durchlauftraegers mit der gleichmaeßiger Abfolge von Stuetz- und Feldmomenten. Das groeßte Stützmoment betraegt im Untergurt 3,55kNm. Die daraus resultierende Spannung betraegt bei einem Widerstandsmoment von 98,4cm³ für ein Rohrquerschnitt und sehr vereinfacht bei 393,6cm³ für den gesamten Untergurt 0,9kN/cm².

Lastfall Verkehrslast (asymmetrisch)

Unter asymmetrischer Belastung zeigt das Bild der Verformung das typische Verhalten eines solchen Tragsystems. In dem Bereich, wo die Belastung auftritt verformt sich das Tragwerk relativ stark, während sich der unbelastete Bereich selbst nicht verformt, sondern sich nur der Verformung des restlichen Systems anpaßt. Das Verhalten der einzelnen Staebe entspricht an sich dem Verhalten unter Volllast. Hoechstens Die Vertikalen im belasteten Tragwerksbereich werden etwas stärker verformt als bei Volllast. Die maximale Verformung tritt im Untergurt mit 0,35cm auf.

Die Bild der Laengskraft gleich an sich auch dem Bild der Laengskraft unter Volllast. Die meisten Vertikalen werden auf Zug belastet um Ober- und Untergurt zusammen zu halten und die Lastabtragung erfolgt ueber die restlichen Vertikalen und die großen Diagonalen. Die lastabtragenden Staebe auf der belasteten Seite des Tragwerks werden natürlich staerker beansprucht als die auf der nicht belasteten Seite. Das auffaelligste Verhalten im Vergleich zum Bild bei Vollast zeigt der Untergurt, der auf der Seite des Tragwerks auf dem keine Last aufliegt zum Auflager hin schrittweise immer stärker beansprucht wird. Die groeßte Laengskraft herrscht im Diagonalstab mit 47,37kN. Die daraus resultierende Spannung betraegt 0,47kN/cm²

Die Momente in den Vertikalstaeben der belateten Tragwerksseite sind analog zu der Verformung etwas staerker als unter Volllast. Die Momente der belasteten Ober- und Untergurtstaebe verlaufen natürlich parabelförmig und sind am groeßten im Vergleich zu allen anderen Staeben. Die Momente auf der unbelasteten Tragwerksseite verlaufen natürlich linear und fallen entsprechend gering aus oder sind nicht mehr zu erkennen. Das maximale Stuetzmoment betraegt im Untergurt 3,58kNm. Die daraus resultierende Spannung betraegt 0,91kN/cm²

Variante 1

Diese Variante ohne Konsolen und doppelte Vertikalstaebe zeige ich auf um die Wirkung dieser Staebe zu verdeutlichen. Das System ist damit nur noch 43-fach statisch ueberbestimmt. Das Bild der Verformung gleicht an sich dem Bild des vollständigen statischen Systems. Der Unterschied der allerdings besteht und durch die weggelassenen Staebe hervorgerufen wird, ist der frueher einsetzende Durchhang am Rand des Systems und die geringer ausfallende und kürzere Hebung in der Mitte des Tragwerks. Die maximale Verformung betraegt 0,56cm gegenueber 0,48cm im originalen System. Nur der Mittelgurt hat jetzt einen viel später einsetzenden Durchhang gegenueber dem originalen System und gleicht jetzt noch mehr einem eingespannten Einfeldtraeger und die Verformung der aeußeren Vertikalen ist jetzt groeßer. Zu erklären ist dies alles ueber die Unterschiede der Verteilung von Druck- und Zugstaeben und die generell kleinere Anzahl an Zugstaeben, wie man es in der Laengskraftdarstellung sehen kann.

Das Bild der Laengskraft gleicht auch dem originalen System. Die Lastabtragung vom Obergurt erfolgt über die aeußeren Vertikalen, die großen Diagonalen und die oberen Abschnitte der inneren Vertikalen. Diese Staebe werden auf Druck belastet. Als Zugstaebe sind nur noch die mittlere Vertikale, die unteren Abschnitte der inneren Vertikalen und die kleinen Diagonlen geblieben um den Ober- mit dem Untergurt zusammen zu halten. Die groeßte Laengskraft hat der untere Abschnitt der großen Diagonalen mit 81,12kN, was einer Spannung von 0,81kN/cm² entspricht.

Die Unterschiede zum vollstaendigen System kann man hauptsaechlich mit einer noch gleichmaeßigeren Abfolge von Stuetz- und Feldmomenten beim Ober- und Untergurt beschreiben.
Außerdem treten in den aeußeren Staeben des Mittelgurtes, in den unteren Abschnitten der großen Diagonalen und in den aeußeren Vertikalen groeßere Momente auf, was auf die schon zuvor beschriebenen Tatsachen der unterschiedlichen Verformungen zurueck zu fuehren ist.
Das maximale Stuetzmoment betraegt jetzt 4,69kNm, was einer Spannung von 1,19kN/cm² entspricht.

Variante 2

Durch die Auskreuzung des letzten rechteckigen Feldes mit einer weiteren Diagonalen erhalten wir ein 49-fach statisch ueberbestimmtes System. Die Verbesserungen die wir im Vergleich zur ersten Variante erhalten, ist eine Stützung des Obergurtes und damit eine verringerte Durchbiegung des Obergurtes. Diese Stuetzung bewirkt auch eine Verringerung der Verformung des Untergurtes, da Ober- und Untergurt immer noch ueber zugbeanspruchte Staebe zusammen gehalten werden. Im Vergleich zum originalen System erhalten wir aber keinen später einsetzenden Durchhang an den Raendern und auch keine laengere Hebung in der Mitte des Tragwerks. Eine Verbesserung des maximalen Durchhangs zum ersten System erhalten wir nicht. Die maximale Durchbiegung betraegt immer noch 0,48cm. Allerdings haben wir diese Durchbiegung mit einer geringeren statischen Ueberbestimmtheit erreicht. Das Verformungsverhalten der aeußeren Vertikalen und des Mittelgurtes ist mit der ersten Variante identisch.

Saemtliche Diagonalstaebe sind jetzt Druckstaebe und stuetzen das Tragwerk zusammen mit den aueßeren Vertikalen, die natuerlilch auch Druckstaebe sind. Alle inneren Vertikalen sind jetzt Zugstaebe und halten Ober- und Untergurt zusammen.
Da wir jetzt zwei Diagonalstaebe zur Lastabtragung mehr haben, ist die Belastung der maximal beanspruchten Diagonalen auch kleiner als im originalen System. Die maximale Laengskraft betraegt nur noch 63,04kN mit einer entsprechenden Spannung von 0,63kN/cm².

Das Momentenbild ist prinzipiell wieder mit der ersten Variante identisch. Im Vergleich zum originalen System ist die Durchbiegung an den Knoten auch nicht kleiner. Allerdings ebenso, wie die Diagonalen die Laengskraft vermindern, so verstaerken sie das Stuetzmoment im Obergurt. Das maximale Stuetzmoment ist auch gegenueber der ersten Variante auf 4,92kNm angestiegen. Dies entspricht einer Spanunng von 1,25kN/cm².

Variante 3

Die dritte Variante als originales Stabwerksystem mit der Einfuegung der Diaginalstaebe aus Variante zwei verknuepft man die Vorteile dieser beiden Systeme. Allerdings ist das Gesamtsystem damit 85-fach statisch ueberbestimmt. Das Verformungsbild ist mit dem Bild der Verformung des originalen Systems identisch. Nur die zusaetzlichen Diagonalstaebe stützen die ca. 5m langen Obergurtsraebe mittig, so daß dort der Durchhang verringert wird. Dies wirkt sich auch auf die Durchbiegung des Untergurtes aus. Die maximale Verformung betraegt jetzt nur noch 0,39cm.

Mit den zusaetzlichen Diagonalstaeben aus Variante 2 haben wir auch in diesem System den Vorteil der besseren Lastabtragung aus dem Obergurt. Vereint mit dem sowieso schon guten Laengskraftverhalten des originalen Systems erhalten wir eine maximale Laengskraft von nur noch 60,78kN und eine entsprechende Spannung von 0,61kN/cm²

Die relativ großen Momente im Mittelgurt, den Vertikalen und den Diagonalen aus Variante zwei sind durch die Vorteile des originalen Systems wieder gesunken. Durch das groeßere Stuetzmoment hervorgerufen von den zusaetzlichen Diagonalen ist das maximale Moment zwar wieder kleiner als in beiden anderen Varianten aber immer noch groeßer als im originalen System. der Wert betraegt jetzt 3,89kNm, was einer Spannung von 0,99kN/cm² entspricht.